Theano中的导数¶

计算梯度¶

Now let’s use Theano for a slightly more sophisticated task: create a function which computes the derivative of some expression y with respect to its parameter x. To do this we will use the macro T.grad. 例如，我们可以计算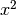 $x^2$ 相对于 $x$ 的梯度。Note that: $d(x^2)/dx = 2 \cdot x$ .

Here is the code to compute this gradient:

>>> import numpy
>>> import theano
>>> import theano.tensor as T
>>> from theano import pp
>>> x = T.dscalar('x')
>>> y = x ** 2
>>> gy = T.grad(y, x)
>>> pp(gy)  # print out the gradient prior to optimization
'((fill((x ** TensorConstant{2}), TensorConstant{1.0}) * TensorConstant{2}) * (x ** (TensorConstant{2} - TensorConstant{1})))'
>>> f = theano.function([x], gy)
>>> f(4)
array(8.0)
>>> numpy.allclose(f(94.2), 188.4)
True

In this example, we can see from pp(gy) that we are computing the correct symbolic gradient. fill((x ** 2), 1.0)表示生成一个与x ** 2相同形状的矩阵并以1.0填充它。

Note

优化器简化符号梯度表达式。你可以通过挖掘编译后的函数的内部属性来看到这一点。

pp(f.maker.fgraph.outputs[0])
'(2.0 * x)'

优化后，图中只剩下一个Apply节点，它让输入乘以2。

我们还可以计算复杂表达式的梯度，例如上面定义的logistic函数。事实证明，logistic的导数是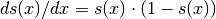： $ds(x)/dx = s(x) \cdot (1 - s(x))$ .

logistic函数的梯度图，其中x轴为x，y轴为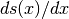 $ds(x)/dx$ 。

>>> x = T.dmatrix('x')
>>> s = T.sum(1 / (1 + T.exp(-x)))
>>> gs = T.grad(s, x)
>>> dlogistic = theano.function([x], gs)
>>> dlogistic([[0, 1], [-1, -2]])
array([[ 0.25      ,  0.19661193],
       [ 0.19661193,  0.10499359]])

一般来说，对于任何标量表达式s，T.grad(s, w)提供Theano表达式用于计算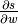 $\frac{\partial s}{\partial w}$ 。这样，Theano可用于对符号进行高效的微分（由于T.grad返回的表达式将在编译期间优化），即使对于具有多个输入的函数也是如此。(see automatic differentiation for a description of symbolic differentiation).

Note

The second argument of T.grad can be a list, in which case the output is also a list. 两个列表中的顺序很重要：输出列表中的第i个元素是T.grad第一个参数相对于第二个参数列表中的第i个元素的梯度。The first argument of T.grad has to be a scalar (a tensor of size 1). 有关T.grad参数的语义的更多信息以及实现的细节，请参见库的这部分。

有关微分内部工作原理的其他信息，也可以在更高级的教程扩展Theano中找到。

计算Jacobian¶

在Theano的用语中，术语Jacobian表示函数相对于其输入的一阶偏导数的张量。（这是对数学中所谓的Jacobian矩阵的泛化。）Theano实现theano.gradient.jacobian()宏，执行计算Jacobian所需的所有内容。The following text explains how to do it manually.

为了手动计算某些函数y相对于某个参数x的Jacobian矩阵，我们需要使用scan。What we do is to loop over the entries in y and compute the gradient of y[i] with respect to x.

Note

scan is a generic op in Theano that allows writing in a symbolic manner all kinds of recurrent equations. 创建符号循环（并优化它们的性能）是一项艰巨的任务，人们正在努力提高scan的性能。我们将在本教程后面回到scan。

>>> import theano
>>> import theano.tensor as T
>>> x = T.dvector('x')
>>> y = x ** 2
>>> J, updates = theano.scan(lambda i, y, x : T.grad(y[i], x), sequences=T.arange(y.shape[0]), non_sequences=[y, x])
>>> f = theano.function([x], J, updates=updates)
>>> f([4, 4])
array([[ 8.,  0.],
       [ 0.,  8.]])

我们在这段代码中使用T.arange生成从0到y.shape[0]的int序列。然后，我们循环该序列，并且在每个步骤，我们计算元素y[i]相对于x的梯度。 scan自动连接所有这些行，生成对应于Jacobian的矩阵。

Note

There are some pitfalls to be aware of regarding T.grad. 其中一个是你不能重写上面的Jacobian表达式为theano.scan(lambda y_i,x: T.grad(y_i,x), sequences=y, non_sequences=x)，即使从scan的文档看来是可能的。原因是y_i将不再是x的函数，而y[i]仍然是。

计算Hessian ¶

在Theano中，术语Hessian具有通常的数学概念：它是由函数的二阶偏导数组成的矩阵，该函数的输出为标量和输入为向量。Theano实现theano.gradient.hessian()宏，完成计算Hessian所需要的所有内容。The following text explains how to do it manually.

你可以类似于类似于的方式手动计算Hessian。现在唯一的区别是，我们计算T.grad(cost,x)的Jacobian，而不是计算某个表达式y的Jacobian，其中cost是某个标量。

>>> x = T.dvector('x')
>>> y = x ** 2
>>> cost = y.sum()
>>> gy = T.grad(cost, x)
>>> H, updates = theano.scan(lambda i, gy,x : T.grad(gy[i], x), sequences=T.arange(gy.shape[0]), non_sequences=[gy, x])
>>> f = theano.function([x], H, updates=updates)
>>> f([4, 4])
array([[ 2.,  0.],
       [ 0.,  2.]])

Jacobian乘以向量¶

有时我们可以用Jacobians乘以向量或向量乘以Jacobians来表达算法。与求值Jacobians然后进行相乘相比，有方法计算所需的结果同时避免对Jacobians进行真正的求值。This can bring about significant performance gains. A description of one such algorithm can be found here:

Barak A. Pearlmutter, “Fast Exact Multiplication by the Hessian”, Neural Computation, 1994

While in principle we would want Theano to identify these patterns automatically for us, in practice, implementing such optimizations in a generic manner is extremely difficult. 因此，我们提供专门用于这些任务的特殊函数。

R操作符¶

R操作符用于求值Jacobian和向量之间的乘积，即 $\frac{\partial f(x)}{\partial x} v$ 。该公式甚至可以推广为x是一个矩阵、或者一个普通的张量，在这种情况下Jacobian变为张量并且乘积变为某种张量的积。Because in practice we end up needing to compute such expressions in terms of weight matrices, Theano supports this more generic form of the operation. 为了求值表达式y相对于x的R操作，将Jacobian与v相乘，你需要做类似这样的事情：

>>> W = T.dmatrix('W')
>>> V = T.dmatrix('V')
>>> x = T.dvector('x')
>>> y = T.dot(x, W)
>>> JV = T.Rop(y, W, V)
>>> f = theano.function([W, V, x], JV)
>>> f([[1, 1], [1, 1]], [[2, 2], [2, 2]], [0,1])
array([ 2.,  2.])

实现Rop操作的列表。

L操作符¶

类似于R操作符，L操作符将计算行向量乘以Jacobian。The mathematical formula would be 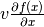$v \frac{\partial f(x)}{\partial x}$ 。L操作符也支持普通的张量（不仅仅是向量）。Similarly, it can be implemented as follows:

>>> W = T.dmatrix('W')
>>> v = T.dvector('v')
>>> x = T.dvector('x')
>>> y = T.dot(x, W)
>>> VJ = T.Lop(y, W, v)
>>> f = theano.function([v,x], VJ)
>>> f([2, 2], [0, 1])
array([[ 0.,  0.],
       [ 2.,  2.]])

Note

v是求值的关键点，其在L操作和R操作中不同。对于L操作符，这个求值的关键点需要具有与输出相同的形状，而对于R操作符，该点应具有与输入相同的形状参数。Furthermore, the results of these two operations differ. L操作符的结果与输入参数具有相同的形状，而R操作符的结果具有与输出相似的形状。

支持R操作的操作的列表。

Hessian乘以向量¶

如果你需要计算Hessian乘一个向量，你可以利用上面定义的操作符，它比实际计算精确的Hessian然后执行乘积更有效率。由于Hessian矩阵的对称性，你有两个选择将给你相同的结果，虽然这些选择可能表现出不同的性能。因此，我们建议在使用以下两种方法之前分析它们：

>>> x = T.dvector('x')
>>> v = T.dvector('v')
>>> y = T.sum(x ** 2)
>>> gy = T.grad(y, x)
>>> vH = T.grad(T.sum(gy * v), x)
>>> f = theano.function([x, v], vH)
>>> f([4, 4], [2, 2])
array([ 4.,  4.])

或使用R操作符：

>>> x = T.dvector('x')
>>> v = T.dvector('v')
>>> y = T.sum(x ** 2)
>>> gy = T.grad(y, x)
>>> Hv = T.Rop(gy, x, v)
>>> f = theano.function([x, v], Hv)
>>> f([4, 4], [2, 2])
array([ 4.,  4.])

最后的要点¶

grad函数以符号的方式工作：它接收并返回Theano变量。
grad可以与宏进行比较，因为它可以重复apply。
标量costs只能由grad直接处理。数组通过重复apply来处理。
内置函数使得高效地计算向量乘以Jacobian和向量乘以Hessian。
优化工作还在进行中，包括有效计算完全Jacobian和Hessian矩阵以及Jacobian乘以向量。